確率の問題って、学校できちんと教わらない場合もあり、ことによると微積よりも難しく感じるかもしれません。

そこで今回は、「高校受験のための中学数学確率講座（シャシャに騙されないために）」と題して、自由掲示板で話題になっていたモンティホール問題をネタに講釈してみようと思います。

そもそも確率とはなんでしょうか？

「部屋を出て最初に出会う人が男である確率は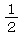である。」という場合、

１．出会う人には男である場合と女である場合と２通りある。
２．そのうち、男である場合は１通りである。

ということを意味しています。つまり、

というわけです。

ただ、これを確率として議論する場合、想定されているあらゆる局面において全ての可能性が等確率で現われるとします。

たとえば、男子校の寮の部屋を出て最初に出会う人が男である確率はほぼ１ですよね。

もちろんこの場合、全ての場合の偏在率を計算に入れて確率の議論を進めることもできますが、ここでは扱いません。

大事なのは

という式です。条件が複雑なように思えても、この単純な式で考えれば「場合の数」を数えるだけで解けます。

さて、自由掲示板で設定されていた問題を簡単に再掲します。

（前提）１０名のＮＰＣのうち１名だけが正解である。
（アクション１）「私」がある１名のＮＰＣに突進しようとする。
（アクション２）地域で８名のＮＰＣについての報告がなされる。その８名の中に「私」が選んだＮＰＣは入っておらず、また正解も入っていない。

この二つのアクションそれぞれについて、場合の数を考えてみましょう。

まずアクション１において、「私」が正解を選ぶ確率は、言うまでもなく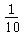ですね。

では正解を選ばない確率は？もちろん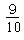です。

これはどういうことかと言うと、

　全ての場合の数：１０通り
　正解の場合の数：１通り
　不正解の場合の数：９通り

という意味です。先程の

で確率が求められるのがわかりますね。

では続いてアクション２です。

８名のＮＰＣについての報告がなされるわけですが、

この報告についてどんな場合が考えられるかというと、

　１．誰かが正解を報告する。
　２．誰も正解を報告しない。

の二種類がありますね。

それともう一つ、重要な要素があります。

　１．私が選んだＮＰＣについて報告がなされる。
　２．私が選んだＮＰＣについて報告がなされない。

というものです。

「正解」も「私が選んだＮＰＣ」も１つです。

では、それが８回の報告に入っているかいないかはどう考えたらいいでしょうか？

この場合は、それぞれの報告に番号を付ければいいのです。

全部で１０回の報告番号を付けてみましょう。

　「ａｂｃｄｅｆｇｈｉｊ」

これで、１０名のＮＰＣ全ての報告番号が決まりますね。

そのうち、実際には８名が報告されるわけですから、最後の「ｉｊ」は報告されないことになります。

もうわかりましたか？

「正解」に与えられる報告番号の全ての場合の数は１０通りです。

そして、それが報告された８名に入らない場合の数は２通りです。

従って、

　１．誰かが正解を報告する。　→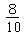　

　２．誰も正解を報告しない。　→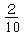　

だということになります。「私が選んだＮＰＣ」についても同様です。

ここから少し難しくなります。

アクション２では、

　８名の報告の中に、「正解」があるかないか、「私が選んだＮＰＣ」があるかないか、

の別々の条件を組み合わせて考えなければならないのです。

実はここでアクション１の結果がどちらであったかが関係してきます。

アクション１で私が正解を選んでいた場合、

「正解」＝「私が選んだＮＰＣ」ですから、

「正解」があるかないかと「私が選んだＮＰＣ」があるかないかとは独立した別々の条件ではなく、単一の条件だということになります。

したがって、

　ａ：アクション１で私が正解を選び、８名の報告の中に正解がない場合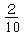　

　ｂ：アクション１で私が正解を選び、８名の報告の中に正解がある場合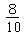　

となります。こちらは簡単ですね。

アクション１で私が正解を選ばなかった場合が複雑です。

８名の報告の中に　私も正解もない。
　　　　　　　　　私があり正解がない。
　　　　　　　　　私がなく正解がある。
　　　　　　　　　私も正解もある。

の４パターンを考えないといけません。

これも先程の「番号付け」で考えてみましょう。先程は「正解」にのみ番号を付けましたから１０通りでした。更に「私」にも番号を付けるとしたらどうなるでしょうか？

先に「正解」に番号が付いている場合、残った番号は９個しかありませんから、「私」に付く番号は９通りです。この二つの場合の数を複合させるにはかけ算をします。

つまり、「正解」「私」のそれぞれの番号の付け方の場合の数は１０＊９＝９０通りです。

この「かけ算」がわかりにくいようでしたら、実際に「正解」と「私」に番号を付けてみるといいでしょう。

正解：ａ　私：ｂｃｄｅｆｇｈｉｊ　９通り
正解：ｂ　私：ａｃｄｅｆｇｈｉｊ　９通り
正解：ｃ　私：ａｂｄｅｆｇｈｉｊ　９通り
正解：ｄ　私：ａｂｃｅｆｇｈｉｊ　９通り
正解：ｅ　私：ａｂｃｄｆｇｈｉｊ　９通り
正解：ｆ　私：ａｂｃｄｅｇｈｉｊ　９通り
正解：ｇ　私：ａｂｃｄｅｆｈｉｊ　９通り
正解：ｈ　私：ａｂｃｄｅｆｇｉｊ　９通り
正解：ｉ　私：ａｂｃｄｅｆｇｈｊ　９通り
正解：ｊ　私：ａｂｃｄｅｆｇｈｉ　９通り
　　　　　　　　　　　　　　　　　９通り＊１０＝９０通り

さて、そのうち私と正解とともに報告からはずれる場合の数は何通りでしょう？

上に全ての場合を尽くしましたから、数えればわかりますが、ｉｊとｊｉの２通りですね。

従って、８名の報告の中に　私も正解もない　確率は　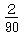　となります。

私があり正解がない場合は、

私がｉｊ以外で、正解がｉかｊのどちらかですから、これも上の表を数えれば　８＊２＝１６通り　だとわかります。

私がなく正解がある場合は、それの裏返して同じ数、　１６通りです。

では、８名の報告の中に私も正解もどちらも含まれる場合の数は？

数えるのがめんどくさそうですが、これは実は、簡単な引き算で出てきます。四種類の場合の数を全部足すと、全ての場合の数になるわけなので、

　９０－（２＋１６＋１６）＝５６通り

というわけです。

まとめると、

　ｃ：１で私が正解を選ばず、８名の報告の中に私も正解もない。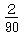　　　

　ｄ：１で私が正解を選ばず、８名の報告の中に私があり正解がない。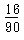　

　ｅ：１で私が正解を選ばず、８名の報告の中に私がなく正解がある。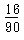　

　ｆ：１で私が正解を選ばず、８名の報告の中に私も正解もある。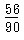　　　

となります。

さて、実際の８名の報告の中には私も正解もなかった、ということでしたから、

このａ～ｆのうちの、ａとｃのみが該当することになります。

　ａ：１で私が正解を選んだ時、８名の報告の中に正解がない場合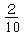　　　

　ｃ：１で私が正解を選ばなかった時、８名の報告の中に私も正解もない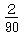　

ということでしたから、これを比べると、ａの方が確率が高いように見えますね。

ですが、この確率には「アクション１」の確率が入っていません。

そもそも１で私が正解を選ぶ確率は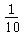、選ばない確率は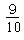でしたから、

それをかけ算すると、

　ａ：私が選んだ方が正解　　→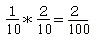　

　ｃ：私が選んだ方が不正解　→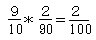　

となって、残った二つのうち、どちらを選んでも（選び直しても）正解する確率は変わらないのがわかりますね。

これが確率の常識です。

さて、モンティホール問題に移ります。

レスにもあったように、これは見識のある数学者がことごとく間違えるという「事件」になったそうです。

というのも、常識的には、残された選択肢のどちらを選んでも正解する確率は同じに見えるからです。そこにこの問題の「罠」があるのだし、その意味でこの問題は確率研究上の大発見だと言えます。

モンティホール問題にはいくつかの成立要件があります。ここでは説明の都合上必要なものだけ挙げます。

それは、「私が選ばなかった選択肢の中から一つを除いてそれ以外が全て不正解だと示す」ということです。

これは極めて作為的なことであり、当初の書き込みにあったような「たまたまそうなった」というものとは全く異なります。

ここの問題で話すと、

　アクション１で私が正解を選んだ　　→　自動的に　ａ　となる。

　アクション１で私が不正解を選んだ　→　自動的に　ｃ　となる。

というものなのです。

この場合の確率は　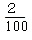　と　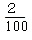　ではありません。

なぜならば、ｂｄｅｆの選択肢は「たまたま起きなかった」のではなく、「システムとして起きないようになっている」からです。つまり、ｂの場合は全てａになるのだし、ｄｅｆの場合は全てｃになるのです。

従って、

　ａ：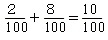

　ｃ：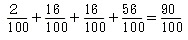

となり、「自分の選択を変更した方が正解率が高くなる」わけです。

数式を使わない別の説明を最後にしてみましょう。

ａｂｃｄｅｆｇｈｉｊのうち、正解がａだったとします。

私が　正解のａを選ぶ確率　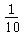　モンティ後ａｘが残る。
私が不正解のｂを選ぶ確率　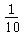　モンティ後ａｂが残る。
私が不正解のｃを選ぶ確率　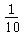　モンティ後ａｃが残る。
私が不正解のｄを選ぶ確率　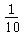　モンティ後ａｄが残る。
私が不正解のｅを選ぶ確率　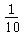　モンティ後ａｅが残る。
私が不正解のｆを選ぶ確率　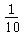　モンティ後ａｆが残る。
私が不正解のｇを選ぶ確率　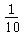　モンティ後ａｇが残る。
私が不正解のｈを選ぶ確率　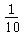　モンティ後ａｈが残る。
私が不正解のｉを選ぶ確率　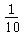　モンティ後ａｉが残る。
私が不正解のｊを選ぶ確率　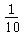　モンティ後ａｊが残る。

さて、選択を維持するのと変更するのとどちらが正解率が高いでしょう？

なお、大事なことなので繰り返しますが、これはあくまで、「作為的なモンティがシステム通りに不正解を開示する」と決められている場合にのみ成立します。

たまたまここまで正解が出なかったんだけど、という場合には成立しません。

つまり、たまたま先に突進した８名が全て不正解を引き当てたとしても、その時に私がトモの前にいたか、キューリの前にいたか、カムの前にいたかは、残りの選択肢の正解率に作用しません。これは常識で考えてよいことです。

もちろん、９名の報告全てが不正解だった場合は、迷わず残りの１名に突進していいでしょう。しかし、そこまで正解が報告されない確率は、実は何の報告も聞かずにいきなり突進して正解する確率と同じなんです。（なので、これが「先着１名」という条件だったら、何番目に突進しようが確率は同じ。）